What Is the Recursive Rule?
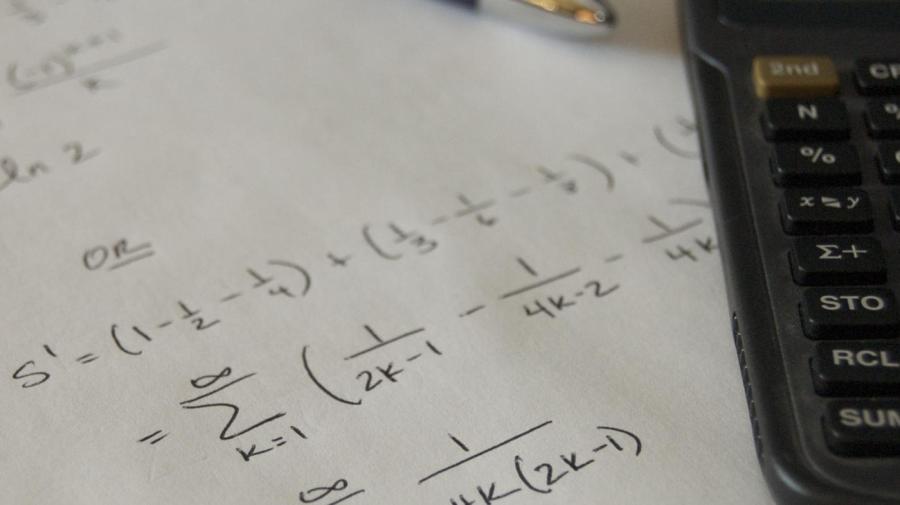
In arithmetic sequences with common difference (d), the recursive formula is expressed as: a_n=a_{n-1}+ d. In a geometric sequence, where the ratio of the given term is constant to the previous term, the recursive formula is expressed as: a(1)=c, a ^n-1, where c is the constant, and r is the common ratio.
The recursive formula is a formula used to determine the subsequent term of a mathematical sequence using one or multiple of the preceding terms. The formula is commonly used in mathematical logic and computer science to define an object with regards to its own properties.
The recursive rule is a formula that states what term is given and what needs to be accomplished to the given term to determine the subsequent term. The recursive rule allows you to determine the next term by formulating a calculation to the previous term. It requires you to determine the value of the term immediately before the term you are attempting to determine.
Most recursive patterns possess a basis, an inductive clause and an external clause. In most recursive problems, only the inductive clause is given to demonstrate the basis or the inductive clause. The Fibonacci sequence is the archetype of linear recursion.





