What Is Function Notation?
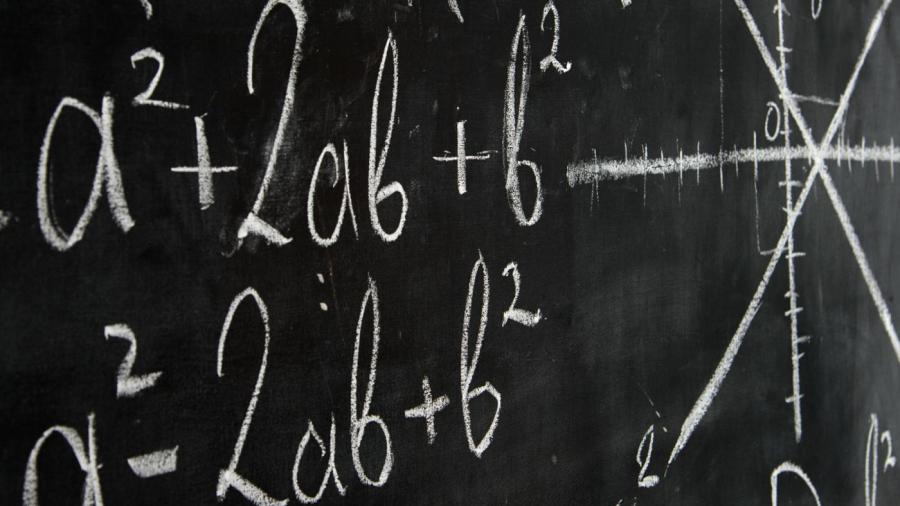
Function notation is a method of writing algebraic variables as functions of other variables. Most often, functions are portrayed as a set of x/y coordinates, with the vertical y-axis serving as a function of x. For example, writing “f(x) = 3x” is the same as writing “y = 3x.”
Writing functional notation as “y = f(x)” means that the value of variable y depends on the value of x. In the simple function “f(x) = x + 3”, y intercepts the y-axis at point (0,3) on the graph, because x is 0 and y is 3. From there, the line is a one-to-one function, with y and x increasing at the same rate. There are also compound functions that are useful in problems requiring more than one set of data. For example, “g(f(x))” means the initial function f is taken, then treated as the original x-value with a new line created on the graph.
Domain and range are two other concepts to understand. Domain refers to the set of independent variables (in most cases, x) for which a function applies. Range refers to the dependent variable, most often y. When writing domain and range, students use curly brackets and write the numbers from least to most, separating them with a comma.





